https://www.acmicpc.net/problem/1699
1699번: 제곱수의 합
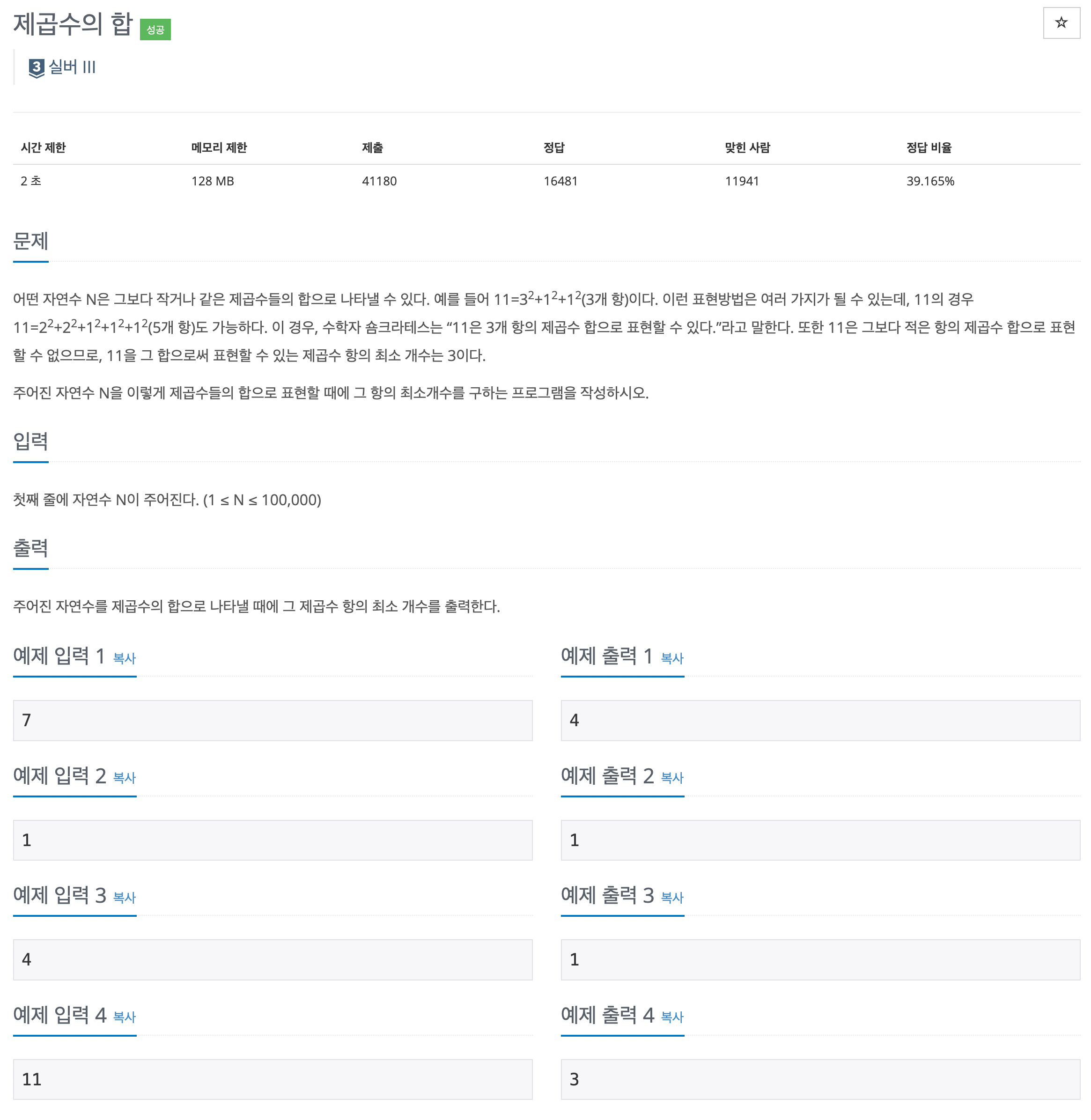
어떤 자연수 N은 그보다 작거나 같은 제곱수들의 합으로 나타낼 수 있다. 예를 들어 11=32+12+12(3개 항)이다. 이런 표현방법은 여러 가지가 될 수 있는데, 11의 경우 11=22+22+12+12+12(5개 항)도 가능하다
www.acmicpc.net
코드 :
dp - topdown
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static final int MAX_INPUT = 100001;
static int[] memo;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
memo = new int[N+1];
// 제곱수들 1로 초기화
for (int i = 1; i <= (int)Math.sqrt(N); i++) {
memo[i*i] = 1;
}
System.out.print(dp(N));
}
public static int dp(int N){
if(memo[N] == 0){
memo[N] = MAX_INPUT;
for (int i = (int)Math.sqrt(N); i >= 0; i--) {
int pow = (int) Math.pow(i, 2);
memo[N] = Math.min(dp(N - pow) + 1, memo[N]);
}
}
return memo[N];
}
}풀이 :
아무리 봐도 답이 안나와서, 많이 검색해서 풀었다. 코드는 내일 다시 정리가 필요하다.
문제를 풀 때, 쉽게 생각하면 가장 큰 제곱수를 사용하는 것이 최소 항의 개수를 구하는 방법이다. 하지만 반례로 12를 예시로 들면,
12 = 3^2 + 1^2 + 1^2 + 1^2 (4개항)
12 = 2^2 + 2^2 + 2^2 (3개항)
12를 나타내는데, 12를 넘지 않는 제곱수 중 가장 큰 수인 3^2(9)를 사용하는 것보다, 2^2를 사용하는 것이 항의 개수가 더 적다. 결국에는 무작정 큰 수부터 항으로 지정한다고 해결되지 않는 문제라는 의미이다.
그냥 dp문제다. 점화식 구하기가 상당히 곤란했는데, 결론부터 말하자면, 제곱수는 어짜피 1개 항으로 나타낼 수 있기 때문에, 주어진 N값에서 제곱수 단위로 빼주면서 memoization 값에 +1 씩 해주면 된다.
위에 12의 예시를 생각하면, 구성할 항에 먼저 3^2을 넣을지, 2^2를 넣을지 모르기 떄문에, 다 넣어보고, dp를 활용하는 것이다.
이해를 위해서 11을 예시로 보면,
11 = 3^2 + 1^2 + 1^2 (3개항)
11 = 2^2 + 2^2 + 1^2 + 1^2 + 1^2 (5개항)
등과 같이 나타낼 수 있다. 1^1로 더 쪼갤 수 있겠지만, 필요없으니 생략했다. 이 두 케이스를 자세히 보면,
11 = 3^2 + 2
11 = 2^2 + 7
위처럼 나타낼 수 있다. 또, 어짜피 제곱수는 1항으로 나타낼 수 있기 때문에, 항의 개수에 주목한다면, 맨 앞에 제곱수들은
11 = 1개(3^2) + 2를 제곱수로 나타낸 항의 개수(1^2 + 1^2)
11 = 1개(2^2) + 7을 제곱수로 나타낸 항의 개수(2^2 + 1^2 + 1^2 + 1^2)
이렇게 생각할 수 있는 것이다. 메모이제이션을 위해 지정한 memo배열이 있고, 거기서 memo[i]는 자연수 i를 제곱수의 합의 최소항의 개수(구해야할 정답)라고 해보자. 그러면 위에 2줄을 다음과 같이 취급할 수 있다.
memo[11] = memo[9] + memo[2]
memo[11] = memo[4] + memo[7]
쓰다보니 복잡해졌는데 주어진 N 값에서 제곱수를 빼면서, memo[N] 값에는 1을 더해주면 된다. N에서 제곱수를 빼고 남은 수(여기서는 2또는 7)는, 제곱수가 아닐수도 있기 때문에 재귀시키면 된다. memo의 값에 1을 더해주는 이유는, N에서 제곱수를 뺐기 때문이다. 제곱수는 자신이 제곱수기 때문에, 제곱수의 합으로 나타내면 최소항의 개수가 무조건 1이다.
만들어지는 memo[N] 중 최소값을 선별하여 저장하면 된다.
점화식 : memo[N] = memo[i*i] + memo[N-i*i]
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 15988번 - 1, 2, 3 더하기 3 (Java) (0) | 2022.03.29 |
|---|---|
| 백준 2225번 - 합분해 (Java) (0) | 2022.03.28 |
| 백준 1912번 - 연속합 (Java 8) (0) | 2022.03.27 |
| 백준 14002번 - 가장 긴 증가하는 부분 수열 4 (Java 8) (0) | 2022.03.27 |
| 백준 11053번 - 가장 긴 증가하는 부분 수열 (Java 8) (0) | 2022.03.26 |




댓글